Ahora demos un vistazo dentro de la "matrix” del control de calidad. Mucho de lo que revisaremos se basa en un fenómeno muy simple que se conoce como Distribución Normal.
Un
estadístico siempre te dirá: “Nada se comporta normal”. Y eso es cierto cuando
se trata de poblaciones u otros grupos complejos. Es probable que des un vistazo
alrededor de tu laboratorio y digas –“Es cierto, nadie se comporta normal”- Sin
embargo, para nuestra fortuna...
...al tomar un grupo de datos, y éstos vienen de muchas mediciones de un mismo material, en condiciones estables y estandarizadas (por decirlo así), observaremos que los datos se distribuyen normalmente.
...al tomar un grupo de datos, y éstos vienen de muchas mediciones de un mismo material, en condiciones estables y estandarizadas (por decirlo así), observaremos que los datos se distribuyen normalmente.
Concepto...
¿Qué significa la distribución normal? Vamos por un ejemplo.
 Subimos al autobús, que nos llevará al lujoso centro de conferencias donde participaremos de nuestras jornadas anuales sobre control de calidad para el Laboratorio Clínico, en
Austria. Al interior del transporte hay una ambiente agradable, gracias a la
climatización del vehículo; pero afuera nos rodea un campo de nieve.
Subimos al autobús, que nos llevará al lujoso centro de conferencias donde participaremos de nuestras jornadas anuales sobre control de calidad para el Laboratorio Clínico, en
Austria. Al interior del transporte hay una ambiente agradable, gracias a la
climatización del vehículo; pero afuera nos rodea un campo de nieve.
Luego de recorrer un buen tramo del camino, y en forma inoportuna, una falla eléctrica en el autobús lo obliga a detenerse y lo peor, debemos descender y esperar afuera. Afortunadamente, algún explorador ha encendido una fogata junto al camino, mientras esperamos la asistencia.
Las reacciones son esperables y en caso de que nadie decida danzar en torno al fuego, observaremos que las personas comenzamos a agruparnos tranquilamente formando un grupo humano que se distribuye normalmente en torno a la
fuente de calor.
La mayor
parte del grupo se dispondrá en un círculo cercano, pero habrán otros pocos que
no alcancen el calor y decidan permanecer más distantes alejándose un tanto
pero siempre distribuidos en torno al centro, ya que es allí donde se decidirán
las cosas que hará el grupo en los siguientes minutos.
 |
| (personas normales distribuidas normalmente en torno a una fogata) |
Nunca
faltará un integrante que decida caminar más lejos, por lo general con un teléfono en la mano. El conductor, instintivamente permanecerá cerca de la cabina de la máquina, con un par de acompañantes solidarios.
Básicamente,
la distribución normal implica que muchos estarán cerca de una “media” (en este
caso representada por la fogata). Y mientras más nos alejemos de esa
media-fogata, será menos probable encontrar a alguien.
Un dato
importante es que la esperanza es infinita. En una distribución normal, siempre
se espera encontrar a alguien aunque sea a kilómetros de la fogata… Aunque se
reconoce esto como sumamente improbable (Ya decía antes que en ciencia
nada es absoluto)
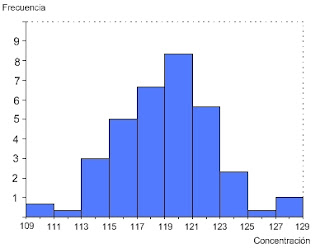
Existe un
gráfico llamado Histograma de
Frecuencias, El cual revisaremos por única vez, ya que sólo nos servirá para
explicar el fenómeno del cual hablamos.
Este
gráfico nos muestra “grupos” (clases), y responde a la pregunta de cuántos
resultados se encontraron entre determinados rangos de valores. Si pensamos en una media de
120, y hacemos grupos de tres en tres. Tendremos una barra que nos indica
cuántos valores hubo entre 109 y 111, otra que nos indica entre 111 y 113… etc.
En la figura podemos observar que se encontraron 5 valores entre 115 y 117. Y también se ve claramente, como los valores se agrupan en torno a la media. De manera que entre 119 y 121, encontramos la mayor cantidad de datos.
La observación importante aquí es que esta tendencia de los valores (a distribuirse en forma normal), se manifiesta mejor mientras más datos existan. Si los datos son muy pocos, este comportamiento podría ser no tan evidente.
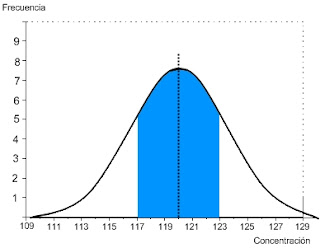
La forma que toma la curva normal, a medida que nos acercamos a infinitos datos, es como sigue:
 Es posible que en una situación normal de fogata, a alguien se le ocurra intentar predecir cuántas personas esperamos encontrar a una distancia determinada de la fogata... Quizá esto suena extraño. Sin embargo si tenemos un grupo de valores distribuidos en forma normal. Con una media y desviación estándar dadas, podremos predecir con cierta seguridad, que cantidad de datos habrá a una determinada distancia en torno a la media.
Es posible que en una situación normal de fogata, a alguien se le ocurra intentar predecir cuántas personas esperamos encontrar a una distancia determinada de la fogata... Quizá esto suena extraño. Sin embargo si tenemos un grupo de valores distribuidos en forma normal. Con una media y desviación estándar dadas, podremos predecir con cierta seguridad, que cantidad de datos habrá a una determinada distancia en torno a la media. Por ello mediremos las distancias en desviaciones estándar, no en las unidades convencionales.
Si la media es 120, y la desviación estándar fuese 3. el valor 123 estaría a 1 desviación estándar de la media. ¿Me explico? (puedes responderme en los comentarios. De hecho, eso me hará pensar que alguien leyó esto)
Hilando más fino. No importa el tamaño de la media o de la desviación estándar. En una distribución normal aproximadamente el 68 % de los datos se moverán no más lejos que 1 desviación estándar (hacia arriba y hacia abajo)
Y si quisiéramos abarcar una cantidad mayor de datos. A nivel de 2 desviaciones estándar, encontraremos aproximadamente el 95.5 % de los valores. En el ejemplo mencionado, esto equivale a decir 120 +/- 6. Entre 114 y 126.
Si queremos asegurarnos aún más, y aumentamos el rango a 3 desviaciones estándar, involucraríamos el 99.7 % de los datos (aproximadamente)
Es imposible abarcar el 100% de los resultados posibles, porque el rango de valores sería infinito. (Insisto, nada en ciencia es 100% seguro).
Por eso, al ampliar el rango, mayor cantidad de valores involucramos. Pero perdemos el entregar un rango acotado.
Si yo defino un rango que comprende 2 desviaciones estándar hacia cada lado, sabré que en condiciones normales aproximadamente un 95.5 % de los datos resultarán dentro de ese rango. Esto también significa que aproximadamente 1 de cada 22 valores excederán los límites por casualidad, sin que nada haya cambiado en el sistema.
Es decir, si yo intento controlar que las condiciones bajo las que están estos valores se han mantenido "normales" o "constantes", y defino un límite de 2 desviaciones estándar, para vigilar que los valores no lo excedan, 1 de cada 22 veces me dará la impresión que se sale de la normalidad, cuando no es así. Esto se conoce como Falso Rechazo
Bien. pongámonos en otra situación. No quiero falsos rechazos, por eso amplío muchísimo los límites. Me encontraré con que aparecen valores lejanos a la media, por causas concretas de anormalidad. No seré capaz de detectar que el sistema cambió, porque he definido límites muy amplios.
Por esto es que regularmente se conoce la regla de +/- 3 DS, como un límite aceptable. Ya que solo 1 de cada 370 valores (aproximadamente). Le superan en condiciones normales. Por lo que el porcentaje de falsos rechazos es aproximadamente 0.03%
Aplicación...
Cuando tenemos que un material control tiene una media y una desviación estándar bajo determinadas condiciones. Podemos representar este valor a medida que se va presentando, sobre una gráfica de Levey & Jennings (Esquema de Shewart). El cual no es otra cosa, que el reflejo de la distribución normal.
Ya detallaremos más acerca de esto, en las siguientes entregas.





GRACIAS, EXPLICACION MUY OPORTUNA
ResponderEliminarmuy buena explicacion. gracias
ResponderEliminar